"Einstein, and the Most Beautiful of All Theories" - BY Avik Dubey
The British theoretical physicist Paul Dirac (1902–1984)
one of the founders of quantum mechanics, once wrote:
“There was difficulty reconciling the Newtonian theory
of gravitation with its instantaneous propagation of forces with the
requirements of special relativity, and Einstein working on this difficulty was
led to a generalization of his relativity — which was probably the greatest
scientific discovery that was ever made.”
General Relativity is generally recognized as a theory
of exceptional beauty. Several tests, along the years, confirmed the
consistency of the theory. I will describe one of the
tests, which correctly explained the
“anomalous” precession of the perihelion of Mercury (see link), which Newton’s theory of gravitation failed to predict.
The
Problem with Newton’s Theory
The precession (or rotation) of the perihelion (the
point in the orbit of a planet that is nearest to the Sun) has a variety of
causes. Two of them are:
·
The presence of the other planets that
causes a perturbation of one another’s orbit, which is the leading cause
·
The oblateness of
the Sun (see figure) which is significantly less relevant
The perihelion rate of the precession of Mercury does not agree with the prediction of Newton’s theory of gravity. This anomaly was noticed by the French astronomer and mathematician Urbain Le Verrier. The final measurement, by Simon Newcomb in 1882, estimated that the actual precession rate disagreed with Newton’s prediction by 43 degrees. Many ad hoc solutions were proposed, but none of them worked.
Using General Relativity to Calculate the Perihelion Precession of Mercury
The Schwarzschild solution is the solution of the
Einstein field equations that describe the geometry of the vacuum spacetime
around the Sun. In other words, the Schwarzschild metric is the metric of the
Solar system caused by the spacetime curvature generated by the Sun. It is
valid when you can:
·
Treat the Sun as a non-rotating object
·
Neglect the gravitational field
originating from the other planets of the Solar system.
The Schwarzschild solution has the following line
element:
Equation 1: The line element of the Schwarzschild solution which describes the geometry of the vacuum spacetime around the Sun.
The parameter R = 2M is
known as the Schwarzschild
radius. The coordinates r, θ, and φ are
spherical coordinates, as illustrated in Fig. 3.
Figure 3: Spherical coordinates (source).
Note that from the isotropy of the metric, we always have θ = π/2 (the orbits are restricted to the equatorial place). In fact, according to the two-body problem (in our case, the bodies are the Sun and the planet), the motion of a body subject to a central force potential will always lie in a plane. Figs. 4 and Fig. 5 show two types of orbiting two-body systems. The motion restricted to the plane is valid in both Newtonian and Einstein gravity theory. Hence, in our analysis, it will be sufficient to consider only geodesics that lie in that plane.
Symmetries in a given spacetime are associated with conserved quantities for particles and photons moving in it. Since the metric g of the Schwarzschild solution is both time-independent (or time translation invariant) and spherically symmetric, the energy of massive particles and the energy of the photon are both conserved. We can see that mathematically as follows.
In a spacetime with metric g, a
free-falling material particle or photon obeys the geodesic equation (the generalization of a “straight line” to curved
spacetime) associated with that spacetime, which is given by (see Schutz):
Note that since photons will also be considered, the
parameter λ cannot be the proper time τ. The geodesic
equation can also be written as:
Now note that:
Eqs. 3 and 4 imply that:
Equation 6: The energy per unit mass of a massive particle and the energy of the photon.
The ~ on top of the massive particle’s energy is used (see Schutz) to indicate that this energy is per unit of mass. In the same vein, as a consequence of the independence of g of φ, angular momentum is conserved. We define:
Equation 8: The three momentum components of the massive particle.
The
momenta for the photon are:
Now intuition tells us to rewrite these equations using effective potentials, namely:
Precession of the Perihelion of Mercury
From now on, let us consider only the motion of massive objects since
our goal is to calculate the precession of the perihelion of Mercury.
A stable circular orbit occurs in the minimum of the effective
potential. Let M be
the mass of the Sun. Differentiating the effective potential, setting the
result to zero and solving for r we
obtain the radius of the stable circular orbit:
Now, in general relativity, a rotating planet does not
return to its initial point. If the relativistic effects are small we should
have an ellipse that slowly rotates around its center. What we can do
(see Schutz) is to examine the motion of the
perihelion of the orbit. To do that we perform three quick calculations
(see Schutz):
·
Derive an expression for dφ/dλ in
terms of angular momentum
·
Derive expressions for dt/dλ in terms
of energy per unit mass
·
Define the new variable u ≡ 1/r
Substituting them in Eq. 10 we get:
We now define y, the deviation
for circularity, as follows:
For a Newtonian orbit, y=0.
To obtain the relativistic expression we substitute Eq. 15 into Eq. 14 and drop
terms of the order of y³. We get the following equation for an almost circular
orbit:
It seems that even Einstein was stunned by the result. After finding the result of the calculation, he could not work for
days. In his own words, he became “beside himself with joy.”
References:-
1. Theories of Relativity- By Albert Einstein.
2. Gravitation & Cosmology- By Steven Weinberg.










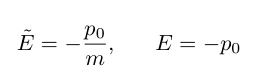
















Comments
Post a Comment